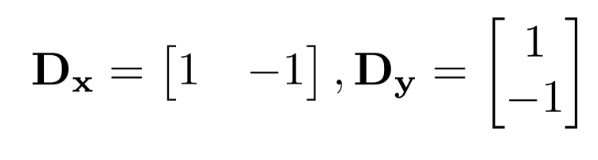
finite difference operator
In this task, I use Finite Difference Operator to convolve the image, calculate the gradient size of each pixel, and finally use a threshold to determine whether a pixel is an edge. If the threshold is large, not all edges can be represented; If the threshold is small, unwanted things may appear. After my adjustments, the output image is as follows:
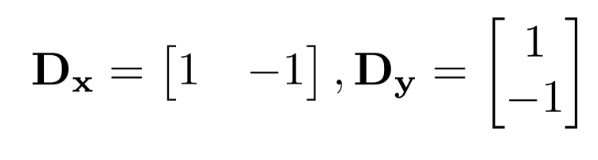
finite difference operator

edge
I used cv2.getGaussianKernel() to obtain a 1D Gaussian kernel and then calculated the outer product of this kernel with its transpose to get a 2D Gaussian kernel. First, I convolved the image with this kernel to produce a blurred image. Then, I applied the Finite Difference Operator mentioned in the previous question to detect edges, followed by thresholding for binarization. If I use the same threshold as in the previous question, not all edges can be detected because the image was blurred; however, when I lowered the threshold, the edge detection improved, and the resulting image became clearer and more continuous.

one step convolve.jpg

two step convolve.jpg
Due to the associative property of convolution, convolving the 2D Gaussian kernel with the Finite Difference Operator first and then applying the resulting convolution kernel to the image will produce the same result.
The image has three RGB channels. For a single-channel image, using the Gaussian filter created earlier and combining them, I obtained a low-frequency blurred image. Then, by using an impulse filter to subtract the Gaussian filter result, I obtained a high-frequency edge image. To sharpen the original image, we simply add the high-frequency image to the original image, making the edge details of the original image clearer. Additionally, we can combine the original image at a ratio of 1 with the high-frequency image at a ratio of n. By adjusting the value of n, we can achieve varying degrees of sharpening (when n = 0, it returns to the original image).

n=0

n=3

n=5

n=10
In fact, we can represent the process of "impulse filter minus the Gaussian filter" using a single filter, as shown in the diagram below. When the sharpened image is blurred and then sharpened again, the overall image still becomes blurry, but many prominent lines appear. This is the result of sharpening the image twice, indicating that sharpening cannot be used for restoring blurry images.

sharp filter
The principle of creating Hybrid Images is to combine the low frequencies of one image with the high frequencies of another, producing an image that appears differently when viewed up close or from a distance. By using a Gaussian filter to extract the low-frequency features of the human portrait and using the method from Part 2.1 to extract the high-frequency features of the cat image, averaging the two images results in a Hybrid Image of both. We can also adjust the ratio of the two, as in Part 2.2, to determine which features—human or cat—are more prominent. Of course, before doing this, the two images must be aligned and scaled to the same size for a better effect. Similar to Part 2.2, perform the same operations on each channel and then combine them at the end.

human:cat=2:1

human:cat=1:1

human:cat=1:5
mushrella

pyramid&zongzi
The Gaussian stack refers to repeatedly convolving an image with a Gaussian filter to obtain a series of increasingly blurred images. The Laplacian stack can be derived by subtracting adjacent images in the Gaussian stack, with the last layer being the same as the last layer of the Gaussian stack. Applying the Gaussian and Laplacian stacks to the apple and orange images results in very blurred images in the final layer. In the middle layers of the Laplacian stack, I obtained edge features ranging from detailed to coarse. After normalizing the edge features and combining the two using an impulse function, the following output was achieved.

stack
First, I tried to blend the two images from left to right. I applied the Laplacian pyramid to both images and used a vertical boundary 01 mask to create a Gaussian pyramid with the same number of layers as the images. In each layer, the two images were combined by weighted addition using the coefficients from the mask, resulting in a blended image for each layer. By summing the images from all layers, I obtained the final blended image.

Orapple
If you want to blend images in other ways, you only need to change the form of the mask, for example:
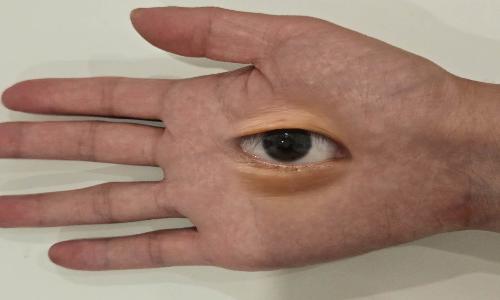
eye on hand

big hand